辛普森殺妻案的機率辯護
- 2020.06.21
- 作者：張右欣
- 數學
- 4401
-
二年級
-
教案分享
-
每周 1 節
-
課程時數 : 1小時
| 學習領域/科目別 | 數學 |
|---|---|
| 核心素養 |
A 自主行動 /
A1身心素質與自我精進
A2系統思考與解決問題
B 溝通互動 /
C 社會參與 /
C1道德實踐與公民意識
|
| 19項議題融入 | 生命, 法治, 閱讀素養 |
2.了解條件機率和機率的差異
3.能透過閱讀資訊來判斷計算條件機率
1994年洛杉磯，美式橄欖球明星、演員辛普森被控告殺害了她的前妻妮克爾.布朗(Nicole Brown)與她的友人羅納德.高曼(Ronald Goldman)，該案被稱為是美國歷史上最受公眾關注的刑事審判案件，辛普森重金聘請了一支由知名律師組成的辯護團隊，媒體稱此辯護團隊為夢幻隊，在經過長達九個月的審判後，辛普森被判無罪，當年檢察方也請來多位專家提供物證鑑識確信必能將辛普森定罪，由有備而來的檢察方對決知名王牌辯護律師的夢幻隊，可以說是一場世紀對決，當年轟動全美，也創下媒體播放審判過程的收視紀錄。
檢方在審判的最初幾周出示證據，證明辛普森曾有對妮可爾的家庭暴力史。檢方想藉以說明辛普森有極高殺妻的動機可能性，但是辛普森的辯護律師Alan Dershowitz則反駁說，只有極少數受到虐待的婦女被其配偶謀殺。
讓我們先看看美國聯邦調查局的犯罪調查資料。
美國聯邦調查局的犯罪調查資料
1.平均2500位受到家暴的妻子，只有1人會被丈夫殺害
2.平均20000名已婚女性中，只有1人會被丈夫以外的人殺害
辛普森的辯護律師Alan Dershowitz主張根據第一點，丈夫因為家庭暴力而殺害妻子的機率只有1/2500（即0.0004%），這是非常小的數字，所以應該忽略辛普森的家庭暴力前科。而檢察方無法反駁這一論點，所以法官認定這家暴前科無法有任何參考價值。
(1) 辯護律師的主張是否有盲點？
讓我們先複習一下條件機率的定義：
P(A|B)=P(A∩B)/P(B) 是在B事件已經發生的條件下，Ａ事件發生的機率。
★例題：
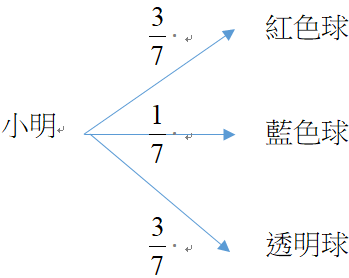
設袋子中有3顆紅球、1顆藍球、3顆無色透明球，今小明隨機從袋子取出一顆球：
(1) 小明取出紅色球的機率
(2) 已知小明取到有顏色的球，求該球是紅色球的機率
★解答：
(1)設小明取出紅色球的事件為A，所求=P(A)，這是一個簡單機率定義問題，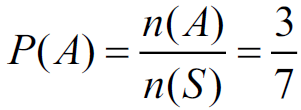
小明取到紅色球的機率為3/7，此機率還不到1/2。
(2)設小明取到有顏色的球的事件為B，取到紅色球的事件為A，
所求為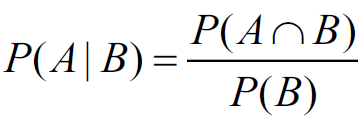
，在這裡是條件機率，
可看出此機率已經大於1/2，而上述計算其實也是貝氏定理的內容。
同學可以藉由這個例子發現機率和條件機率可以有很大的落差，這個例題多數學生都能理解並獨力計算出解答。讓我們回到辛普森案的審判現場，各位同學是否已經發現出律師的所主張的機率盲點了？
(2) 辯護律師的盲點說明
辦護律師所引用的數據是機率，乃是針對所以還活著的已婚受家暴婦女，然而實際上辛普森的老婆已經死了，因此在這裡我們應該是用條件機率來計算辛普森殺害老婆的機率，由調查局資料第二點: 平均20000名已婚女性中，只有1人會被丈夫以外的人殺害，不妨就一般常理的角度認知，「已婚女性被丈夫以外的人謀殺與該已婚女性被家暴是獨立的」，換句話說平均20000名已婚且被家暴的女性，只有1 人會被丈夫以外的人殺害，也就是機率為1/20000， 今天辛普森的妻子已經死亡了，這是已經發生的條件，所以我們要計算的機率不是家暴婦女被丈夫殺害的機率，而是在已知家暴婦女被殺害的條件下，此婦女被丈夫殺害的機率，可以由樹狀圖來求P(辛普森殺害妻子|家暴妻女被殺害)
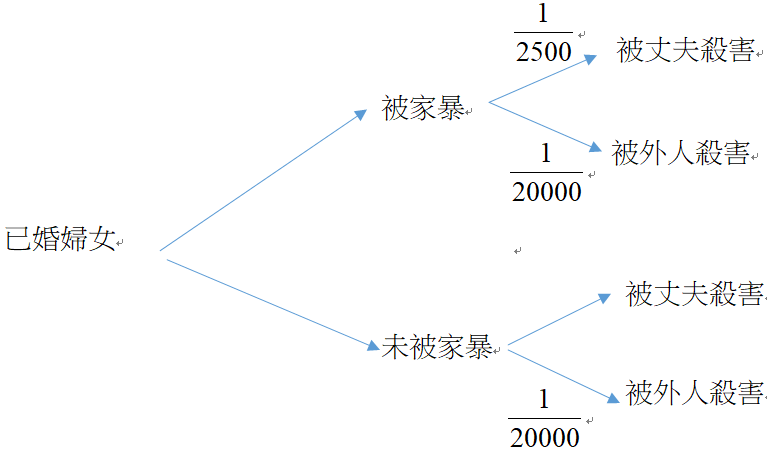
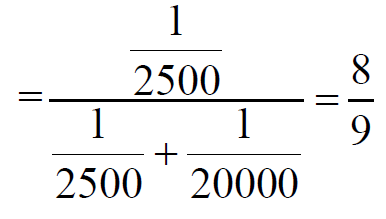
上述計算可以看到條件機率是8/9，說明了辛普森在條件機率下是有很高的殺妻可能性，所以如果檢察官數學好一點，就能輕易反駁辦護律師的主張，這個例子也讓我們發現日常生活中我們習慣用機率的思維來思考問題，容易忽略何時該用條件機率來面對問題。
請根據以下3點犯罪調查資料來回答問題：
(1)平均2500位受到家暴的妻子，只有1人會被丈夫殺害。
(2)平均20000名已婚女性中，只有1人會被丈夫以外的人殺害。
(3)平均20000名已婚女性中，只有200 人會受到家暴。
問題1
若已婚婦女被丈夫以外的人殺害，則該婦女有受到家暴的機率？
問題2
平均兩百萬名已婚婦女，有多少位被丈夫以外所殺害的婦女是未受到家暴的？
問題3
試求已婚女性被家暴且被丈夫殺害的機率？
問題4
若在已婚女性被殺害的條件下，此婦女被丈夫殺害的機率為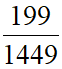
，試求已婚女性被丈夫殺害的機率？
※學習單解答位於上方「規劃內容」區塊中的授課計畫表