貝茲曲線-積分
- 2021.12.18
- 作者:授課橘數學小編
- 數學

- 4038
| 學習領域/科目別 | 數學 |
|---|---|
| 情境範疇 | 甲 -6 積分/ 甲 -7 積分的應用 |
題幹
坐標平面上,由A、B、C、D四點所決定的「貝茲曲線」(Bézier curve)指的是次數不超過3的多項式函數。其圖形通過A、D兩點,且在點A的切線通過B,在點D的切線通過點C。令y=f(x)是由A(0,0)、B(1,4)、C(3,2)、D(4,0)四點所決定的「貝茲曲線」。
| 問題一 |
(1)設y= f(x)的圖形在點D的切線方程式為y=ax+b,其中a、b為實數,求a、b之值。
(2)試證明多項式f(x)可以被x2-4x整除。 (3)試求f(x)。 (4)求定積分 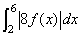 之值。 之值。
參考答案 :
請見「試題概念與分析」
搭配學習內容/學習表現 :
F-12 甲 -6 積分/ F-12 甲 -7 積分的應用。f-V-9 理解定積分的原理,並能用以溝通、推論和解決問題。 f-V-8 認識微分與積分互為逆運算,理解微積分基本定理的意義,並能用以推論。 f-V-2 認識多項式函數的圖形特徵,理解其特徵的意義,認識以多項式函數為數學模型的關係或現象,並能用以溝通和解決問題。 試題概念與分析 :

|
|---|
延伸閱讀材料
| 文章 | 普高數學素養試題超展開 VOL.12 |
|---|
推薦相關文章
留言
